| Info | ||
|---|---|---|
| ||
While addressing a sub-optimal performance issue for interpolation from the octahedral reduced Gaussian grid introduced with IFS cycle 41r2 to regular latitude-longitude grids, a problem was discovered with the method used to calculate the longitudinal points in the source grid. In some specific cases, this problem leads to an incorrect computation of interpolation weights and hence to incorrect interpolated values at some points of the output grid. The problem affects all versions of EMOSLIB prior to version 4.3.0. The problem is also present in fields retrieved with versions of MARS (including the WebAPI) that use any EMOSLIB version prior to version 4.3.0, Metview versions prior to 4.6.1 and for disseminated products from IFS cycle 41r1 and earlier. This page provides information about the problem and the specific cases where differences can occur. |
| Table of Content Zone | ||||
|---|---|---|---|---|
|
Description of the problem
The problem originates in the calculation of the longitude values of the source grid in EMOSLIB routines IRDIWE and IGDIWE. These routines use an integer value of the longitudinal grid increment (the 'stride') which, in some cases, results in a truncated value of the increment. This can result in an error in the computation of the longitude values for points in the source grid.
- The error occurs at specific latitude lines, j, with Nj longitude points whenever the grid spacing Dj=360/Nj has a remainder smaller than 10 microdegrees (1/100000 of a degree).
- The error accumulates linearly from 0° to 360° along the line of latitude.
- The error is minimal at grid points to the east and maximal at those to the west of the 0° meridian.
- The error is larger the greater the number of longitude points (Nj) along the line of latitude.
When the input grid is an original reduced Gaussian ("N-grids"):
- the error occurs at bands of consecutive lines of latitude that have the same Nj.
- generally, the error is largest away from the equator (at about 20° N and 20° S for the N640 grid).
When the input grid is an octahedral reduced Gaussian ("O-grids"):
- the error can occur at almost all lines of latitude because the Nj changes continuously
- the error is largest close to the equator where the resolution is highest.
In situations where the error occurs, the incorrect computation of the longitude values leads to two issues:
- The longitude points in the source grid are computed incorrectly. This leads to an incorrect computation of interpolation weights and hence to incorrect values at some points of the output grid.
- The nearest grid points used for the interpolation may be incorrectly identified due to a numerical 'shift' of the input grid cell.
The error is most evident for parameters where the gradient of the field is large and where a change in the nearest grid points or the interpolation weights used thus has a larger effect.
The error also affects the identification of points used for the land-sea mask processing of surface fields.
Which interpolations are affected ?
The problem affects interpolations from:
- input original reduced Gaussian grid point fields to output regular Gaussian or regular latitude-longitude grids (without rotation)
- input octahedral reduced Gaussian grid point fields to output regular Gaussian or regular latitude-longitude grids (without rotation).
Which interpolations are not affected ?
- Interpolations to rotated latitude-longitude grids are unaffected
- Transformations from spherical harmonic components to grid point fields are unaffected.
- Interpolations of wave (WAM, ENS-WAM etc) fields are unaffected.
For which cases is the problem fixed ?
The problem is fixed in EMOSLIB version 4.3.0 and newer for the following cases:
- interpolations from original reduced or octahedral reduced Gaussian grids to global, unrotated regular Gaussian grids (gridType=regular_gg);
- interpolations from original reduced or octahedral reduced Gaussian grids to global, unrotated latitude-longitude grids (gridType=regular_ll).
For the Disseminated products from IFS cycle 41r2, the problem is also fixed for interpolations to sub-areas of regular latitude-longitude grids
In addition, the problem is fixed for interpolations from original reduced or octahedral reduced Gaussian grids to sub-areas of unrotated regular Gaussian grids or regular lat-lon grids at EMOSLIB 4.3.7.
For which cases does the problem still exist ?
The problem has not been fixed for the following cases::
- interpolations from sub-areas of regular Gaussian grids or unrotated regular latitude-longitude grids;
- interpolations from global "staggered" regular lat-lon grids (i.e., global grids that are not centred on 0° latitude and 0° longitude).
In which software versions is the problem fixed ?
The problem is fixed in EMOSLIB version 4.3.7 and newer. This is used by:
- MARS client updated on 9 February 2016
- Metview version 4.6.4 and newer
- Disseminated products for IFS cycle 41r2 (implemented 8 March 2016)
Can results obtained with EMOSLIB 4.3.x be compared with the old version ?
Users can check results with the previous versions of MARS by using 'mars -t -p'. This version of MARS uses EMOSLIB 4.2.2 which does not include the bug fix.
| Warning |
|---|
The 'mars -t -p' version is provided for testing purposes only. It should not be used as a long term replacement for the default 'mars' version. Please let ECMWF know if you need to use 'mars -t -p'. |
Examples
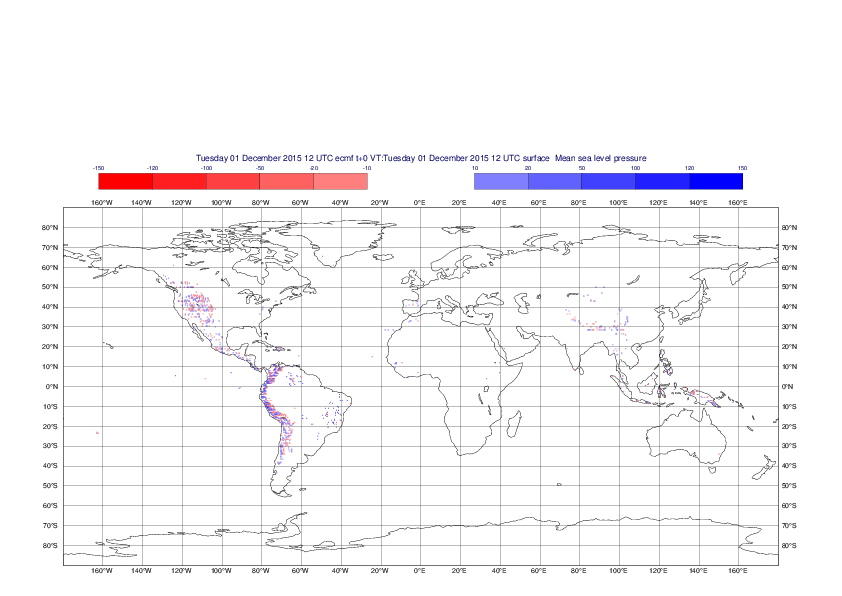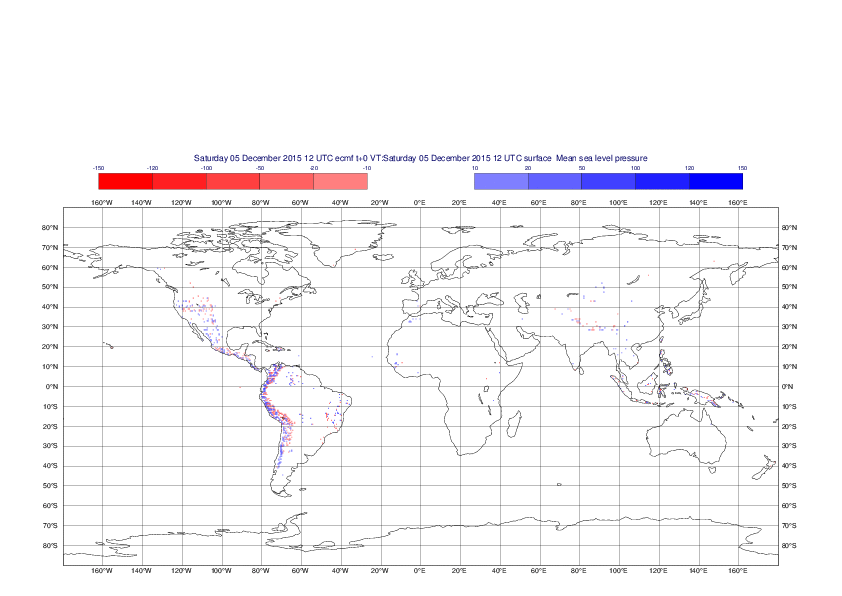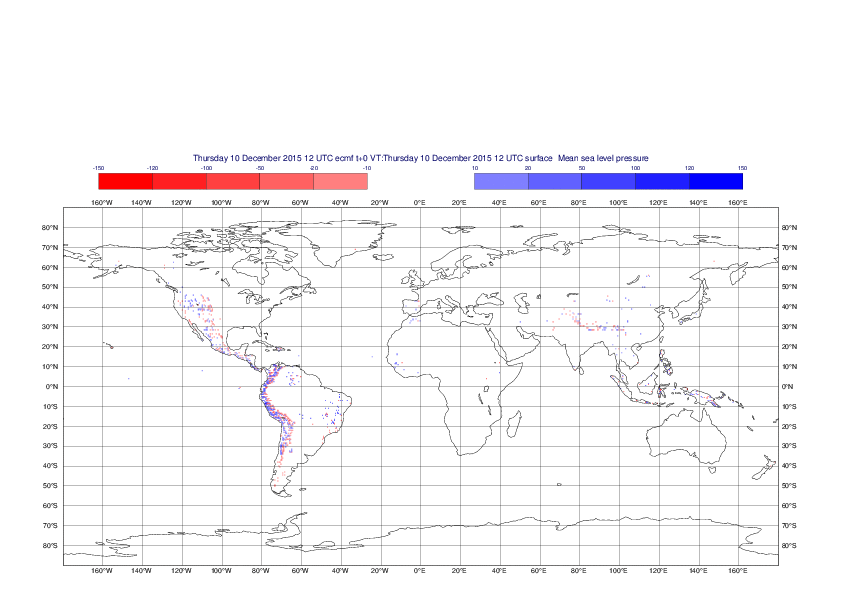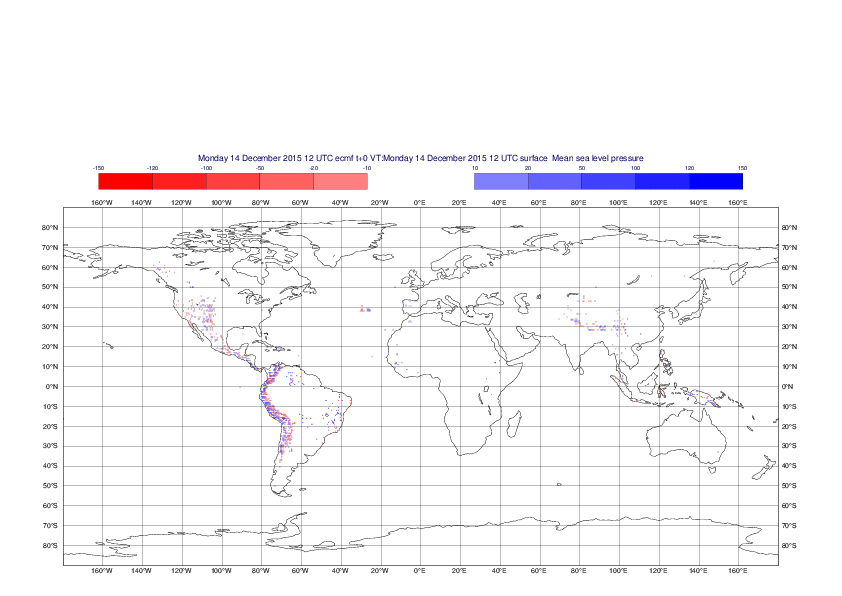
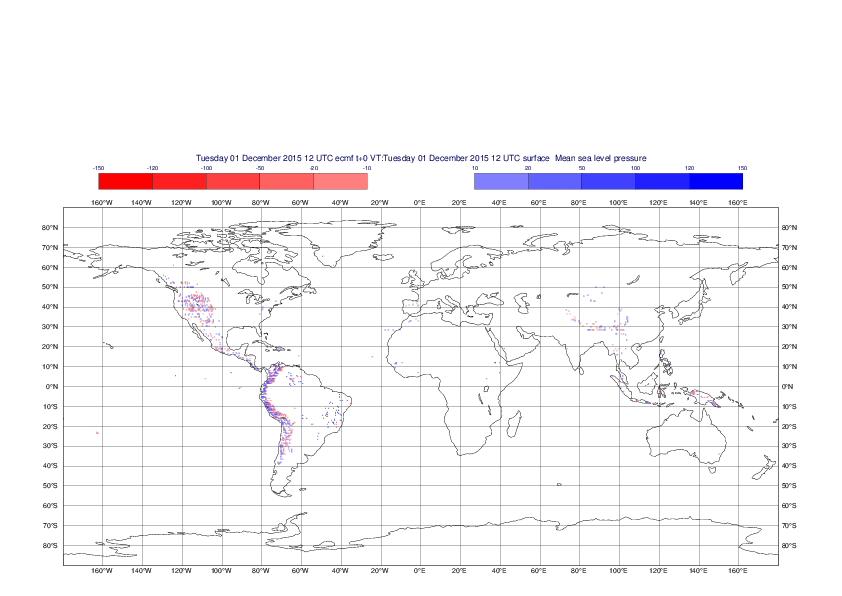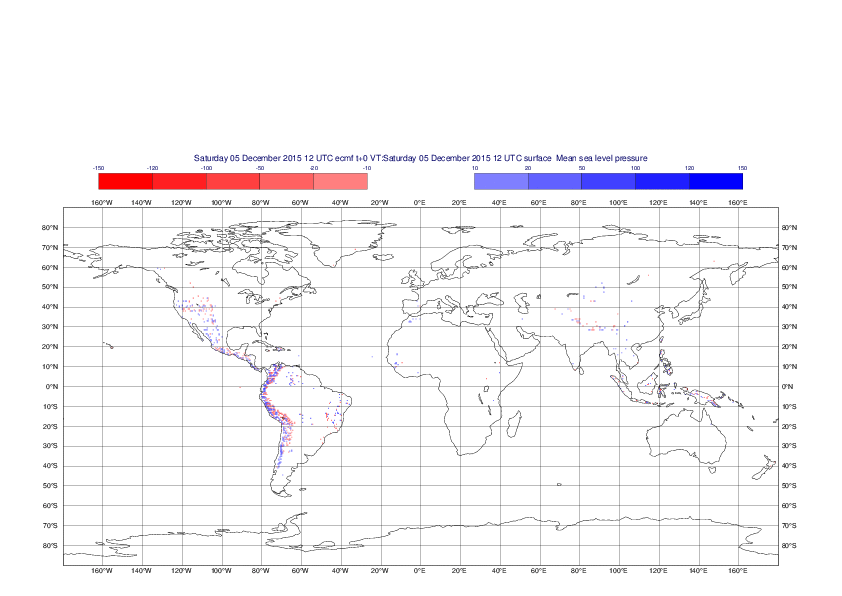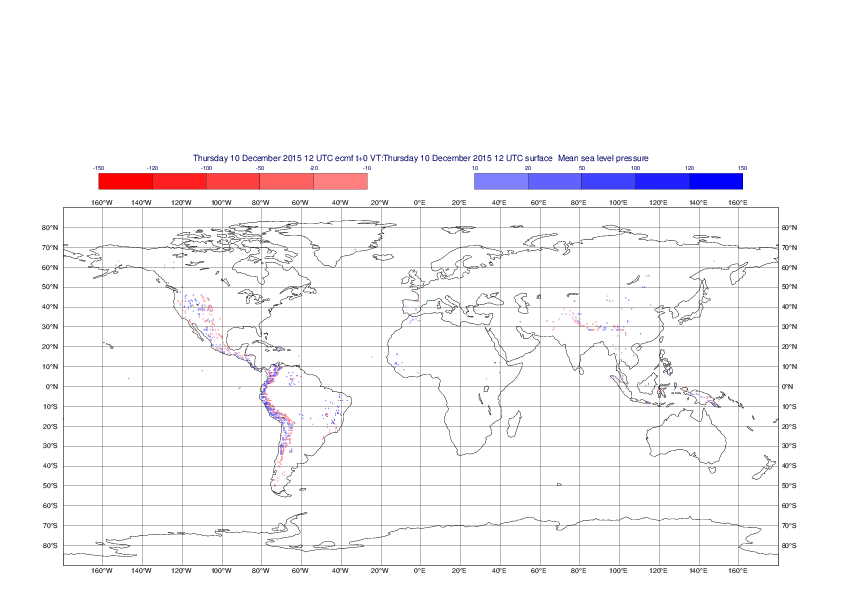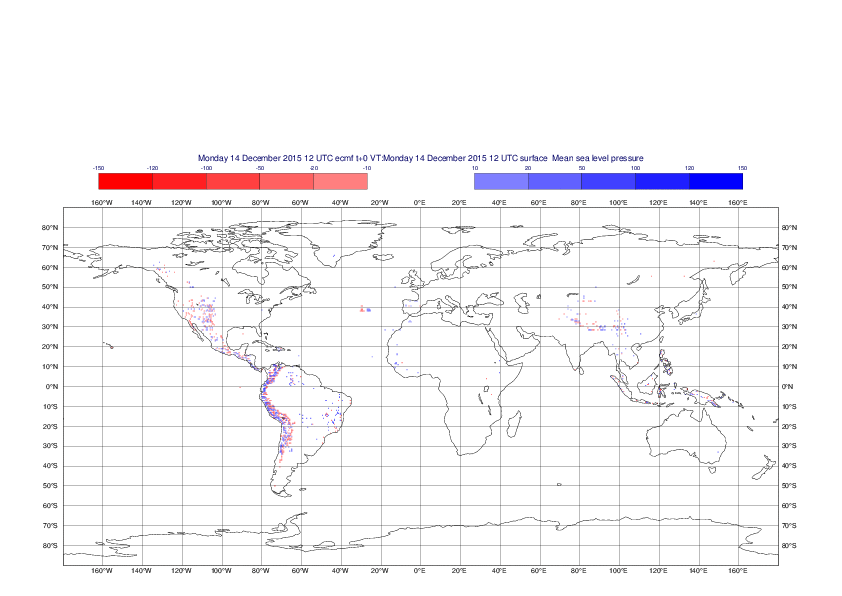
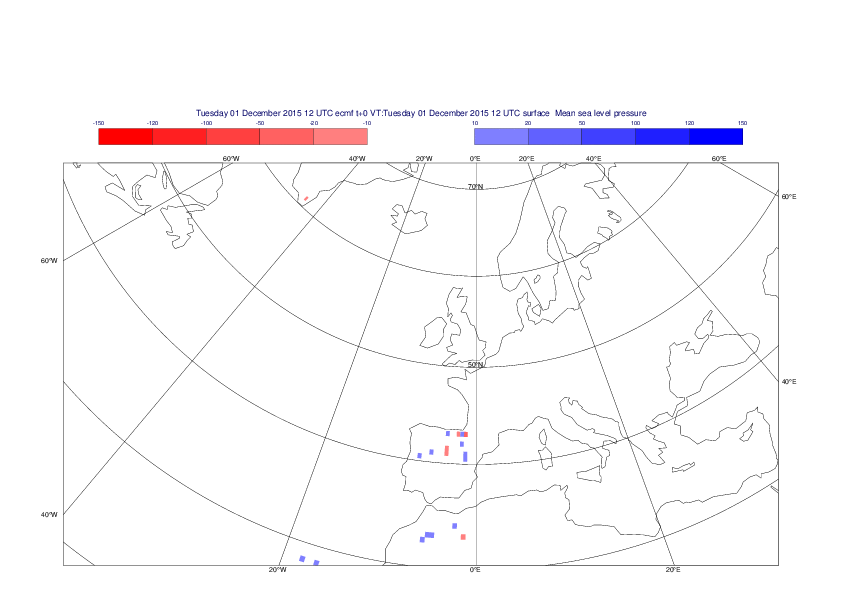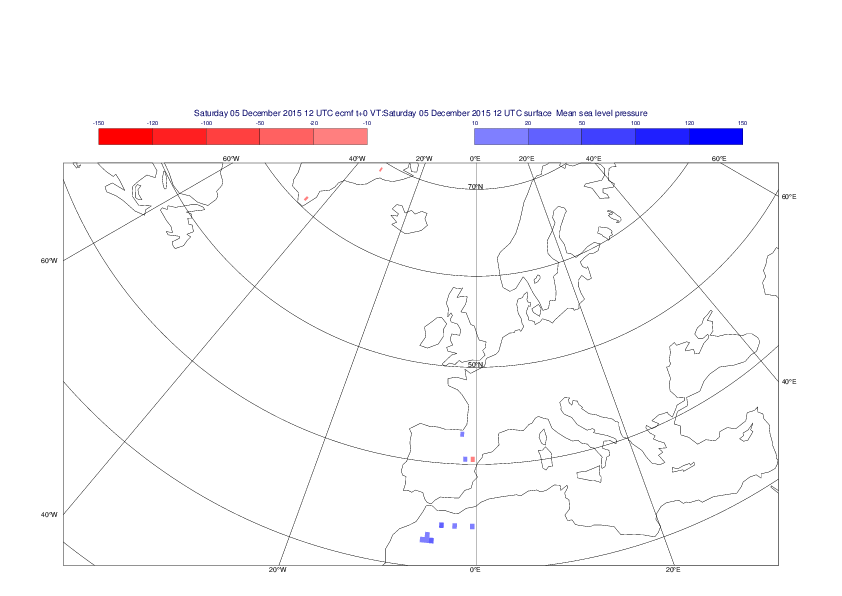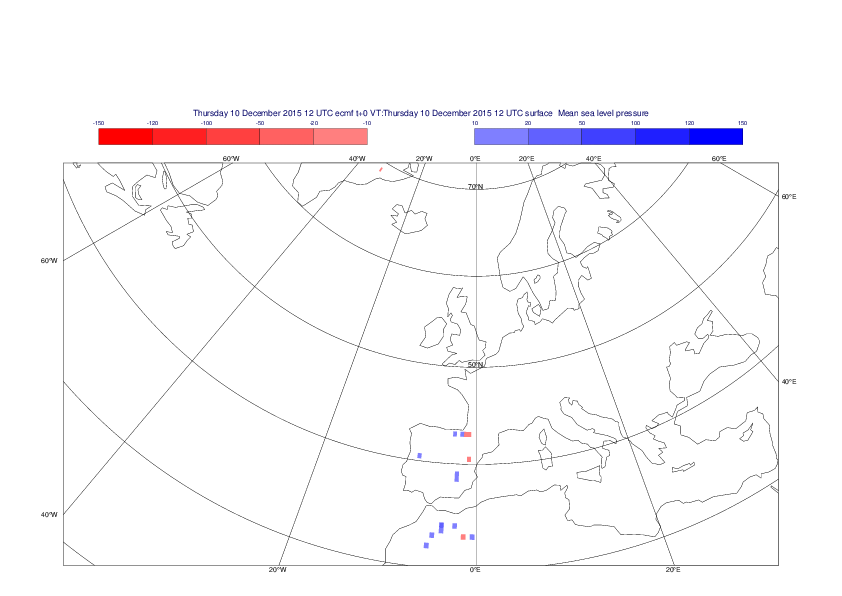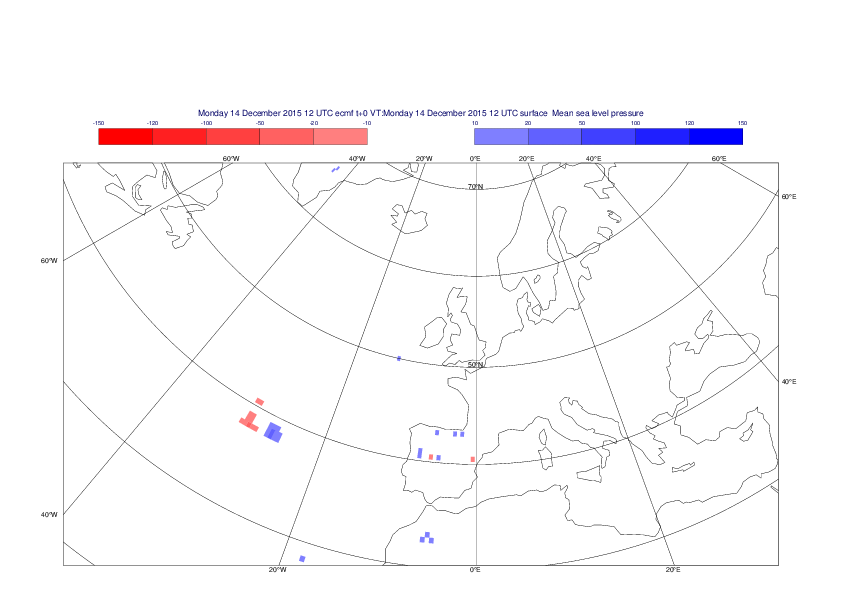
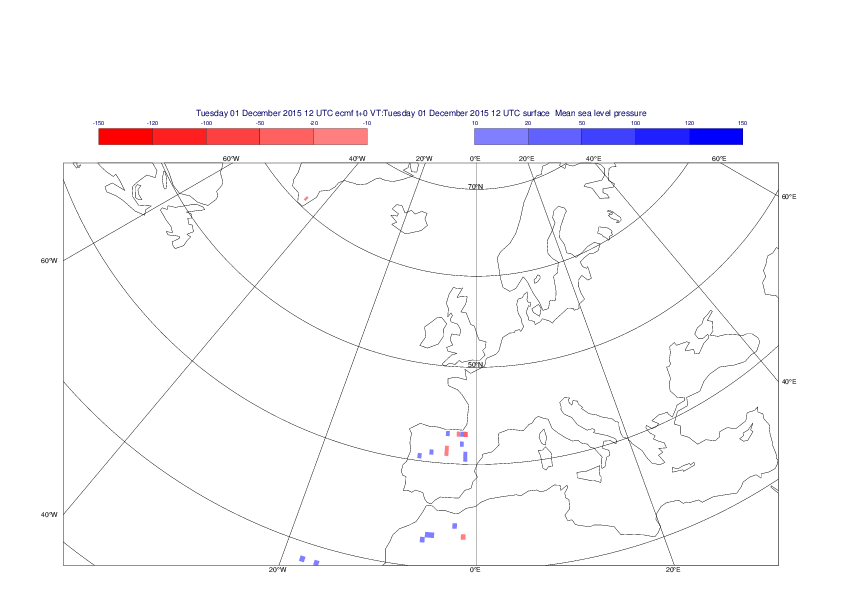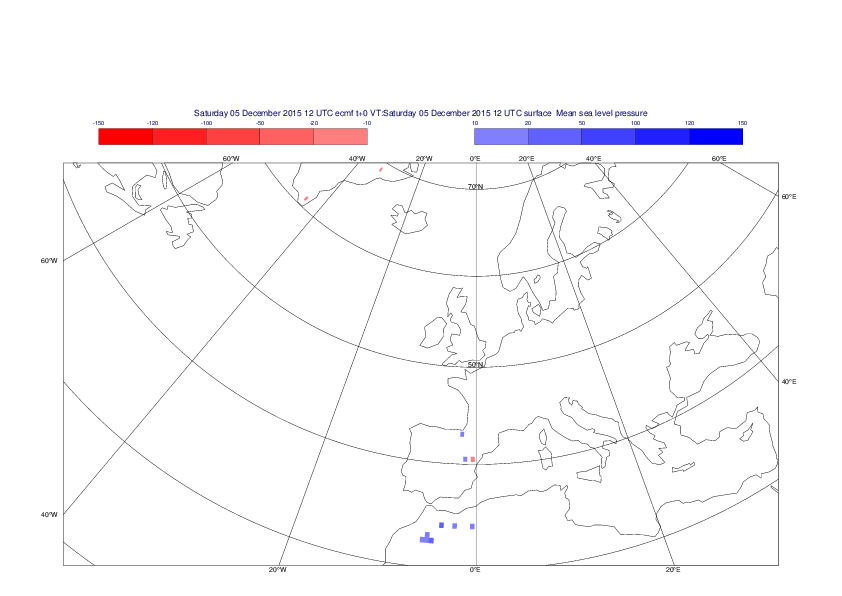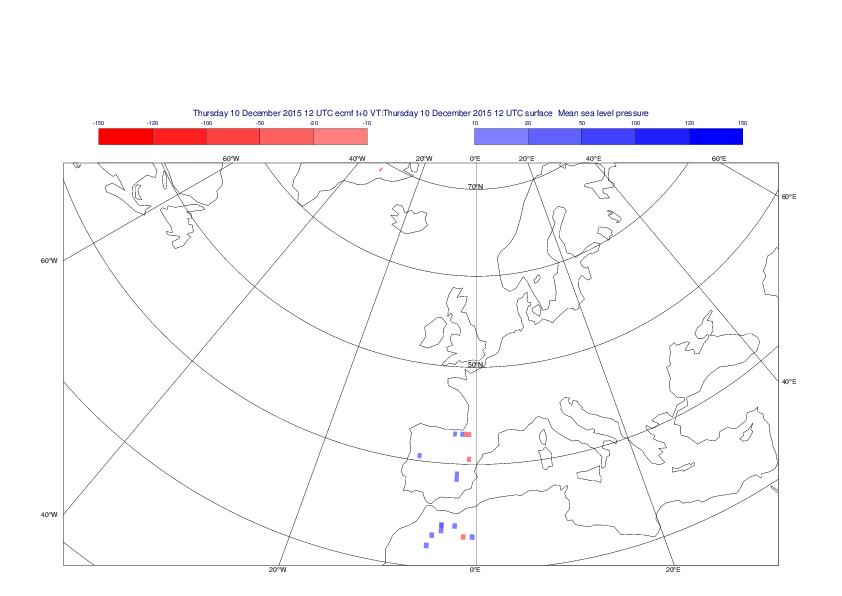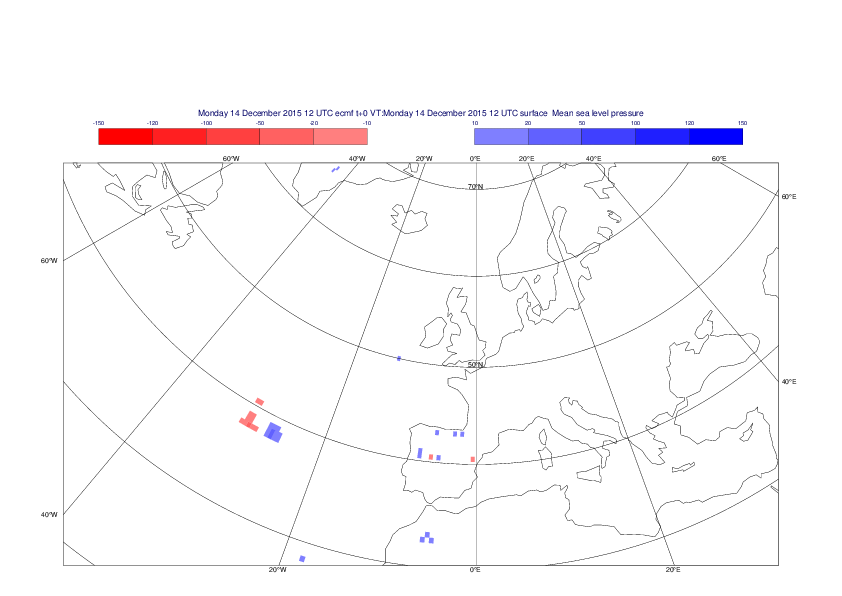
Mean sea-level pressure
The plots show the differences between the new interpolation method implemented in EMOSLIB version 4.3.0 and the old method for the interpolation of the mean sea-level pressure from the reduced Gaussian grids to a 0.5°x0.5° regular latitude-longitude grid for the period 1-14 December 2015.
For this field the differences are:
- between -49.26 Pa and 37.76 Pa for interpolation from an the N640 original reduced Gaussian grid to a 0.5°x0.5° regular latitude-longitude grid
- between -169.26 Pa and 146.26 Pa for interpolation from an the O1280 octahedral reduced Gaussian grid to a 0.5°x0.5° regular latitude-longitude grid
The plots in the upper panels show differences at the global level while those in the lower panels show the same fields plotted over the Europe area in a polar stereographic projection.
| Section | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
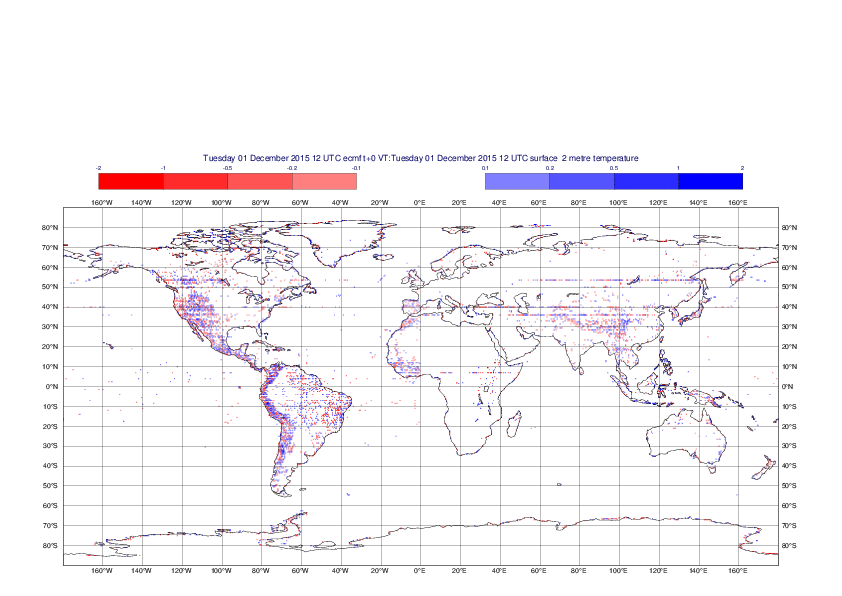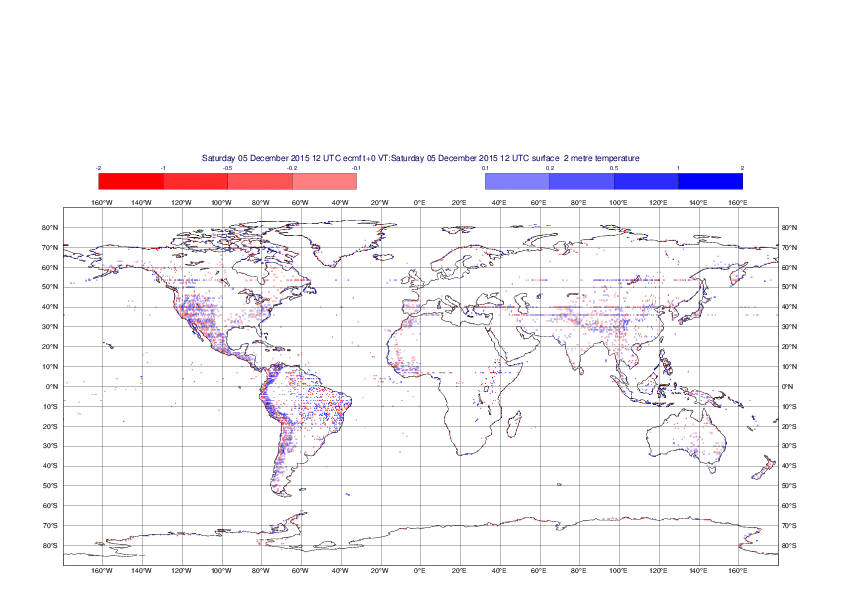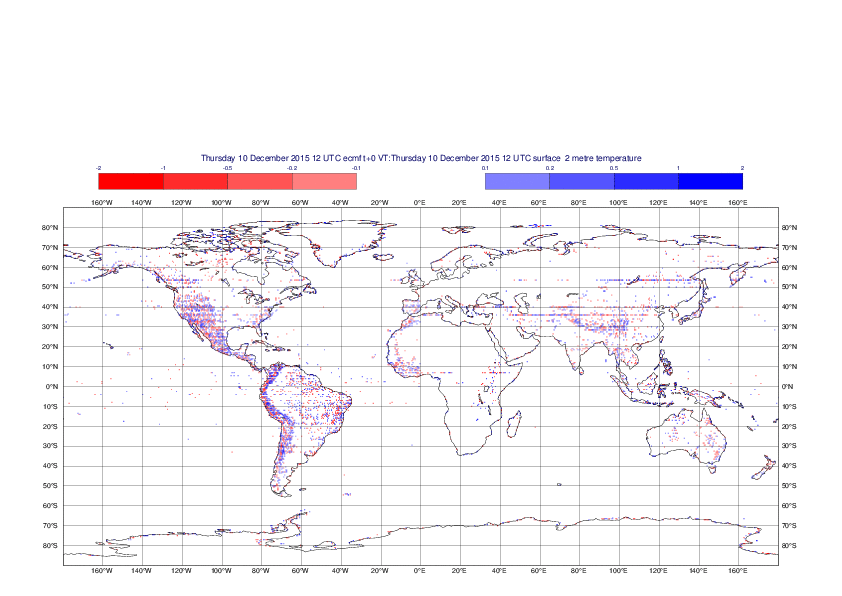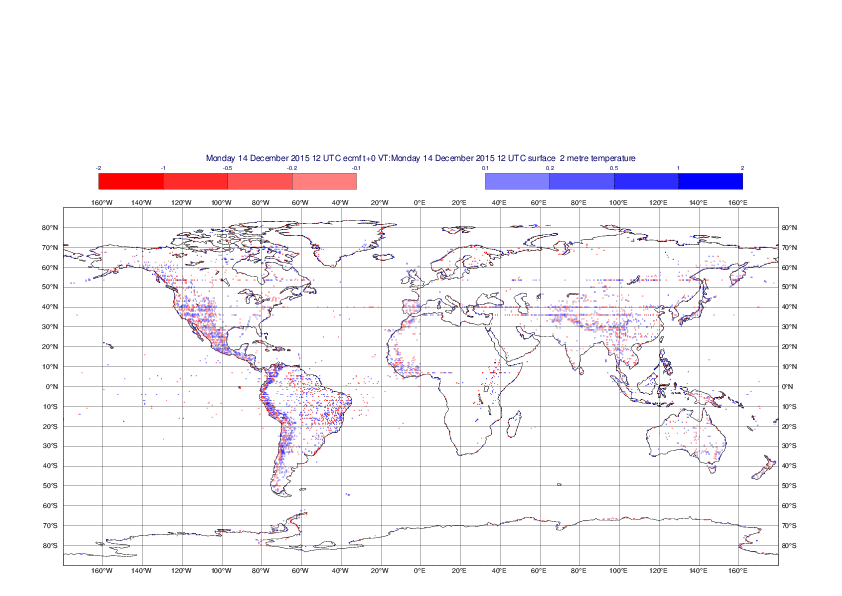
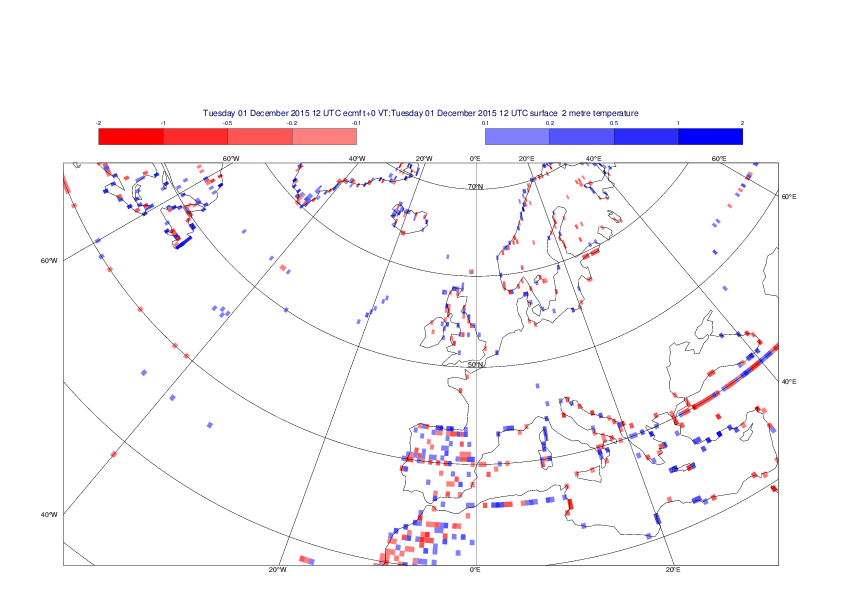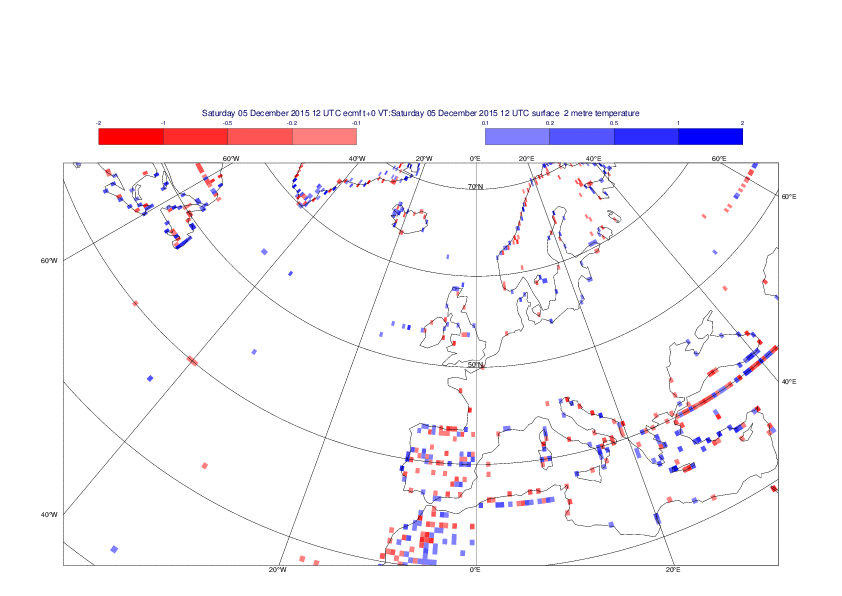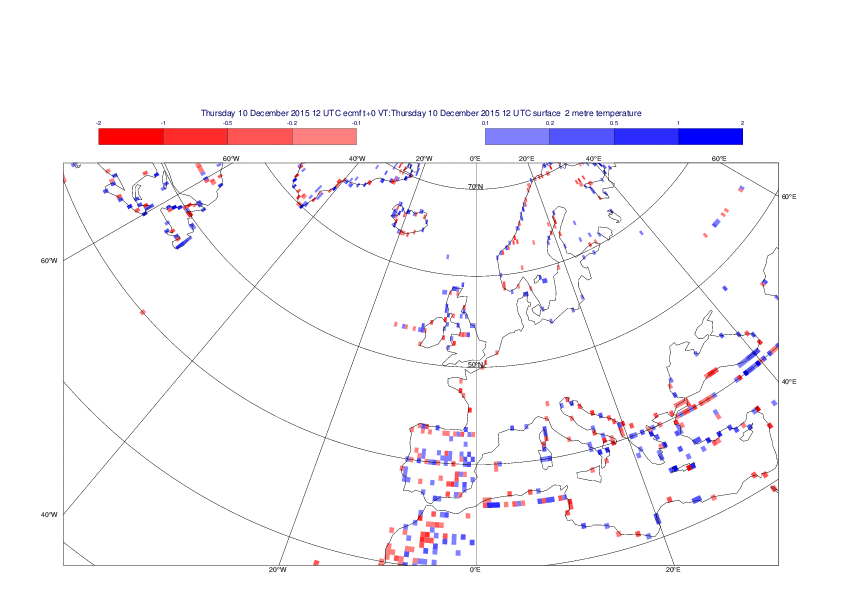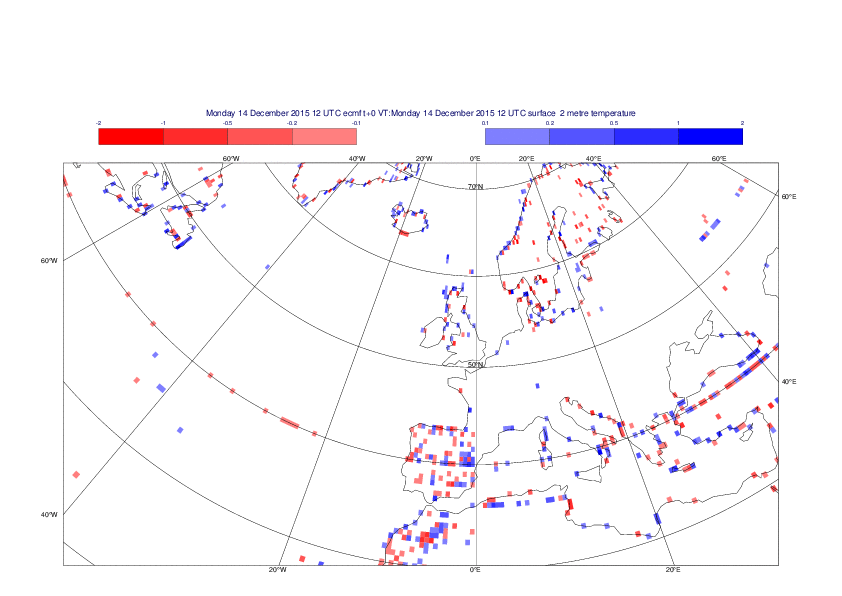
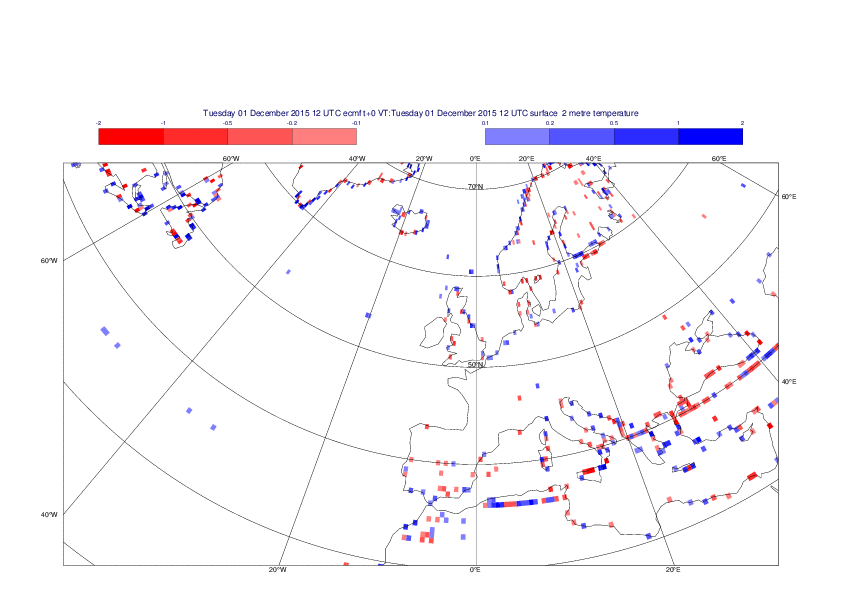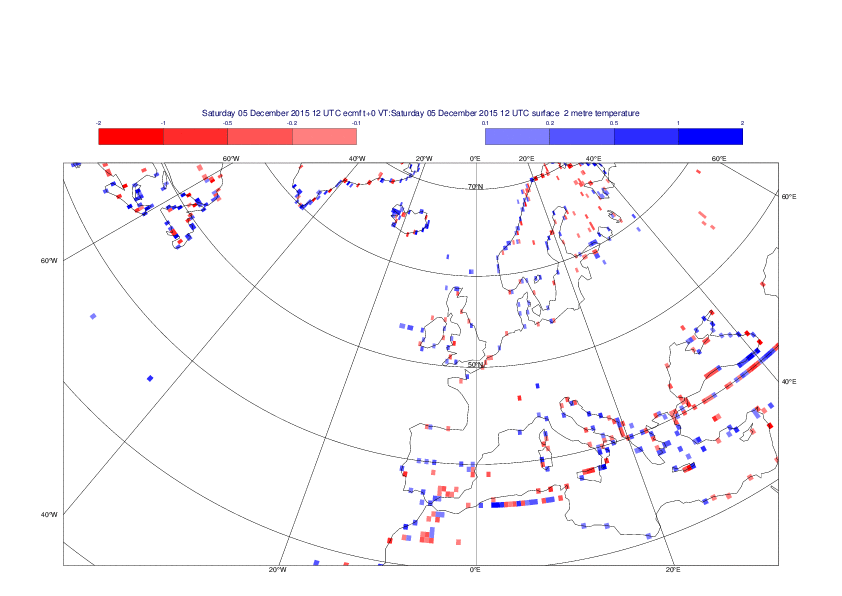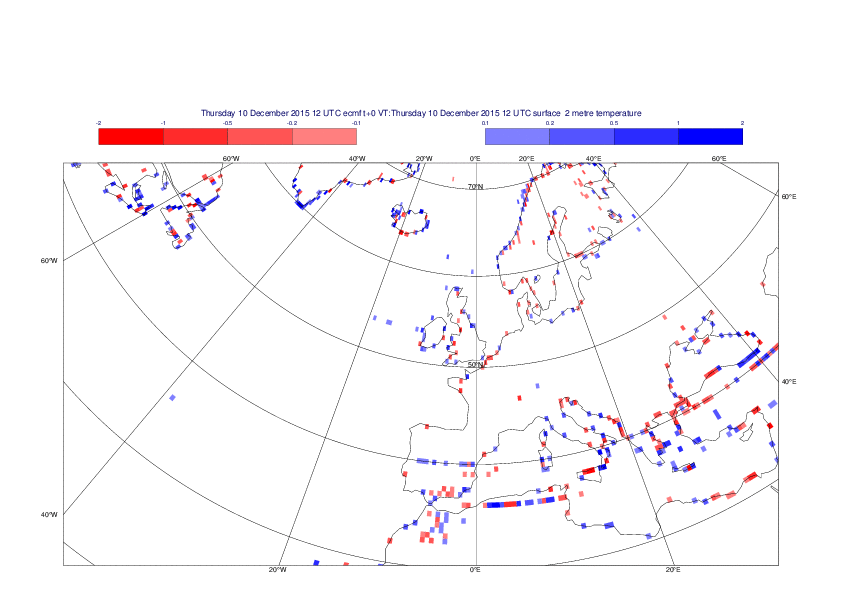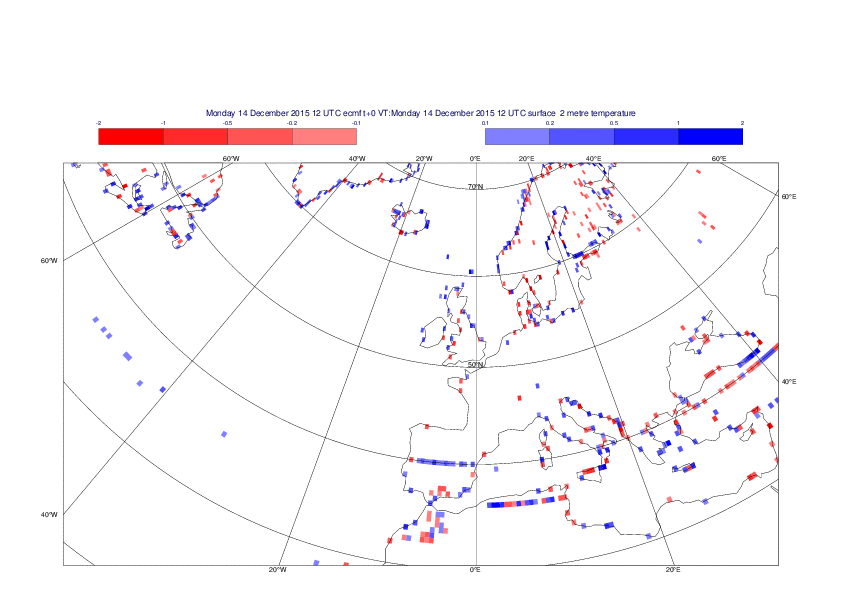
2 metre temperature
The plots show the differences between the new interpolation method implemented in EMOSLIB version 4.3.0 and the old method for the interpolation of the 2m temperature from the reduced Gaussian grids to a 0.5°x0.5° regular latitude-longitude grid for the period 1-14 December 2015.
For this field the differences are:
- between -8.21 K and 4.79 K for interpolation from an the N640 original reduced Gaussian grid to a 0.5°x0.5° regular latitude-longitude grid
- between -3.62 K and 4.44 K for interpolation from an the O1280 octahedral reduced Gaussian grid to a 0.5°x0.5° regular latitude-longitude grid
| Section | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|