Naming convention
The Gaussian grids are defined by the quadrature points used to facilitate the accurate numerical computation of the integrals involved in the Fourier and Legendre transforms. The grids are labelled by N where N is the number of latitude lines between the pole and the equator. For example, for the N=640 Gaussian grid, there are 640 lines of latitude between the pole and the equator giving 1280 latitude lines in total.
The grid points in latitude, θk , are given by the zeros of the Legendre polynomial of order 2xN (i.e., the total number of latitude lines from pole to pole): P 2N 0 (μk=sinθk) = 0. A consequence of this is that a Gaussian grid has:
- latitude lines which are not equally spaced;
- no latitude points at the poles;
- no line of latitude at the equator;
- latitude lines which are symmetric about the equator.
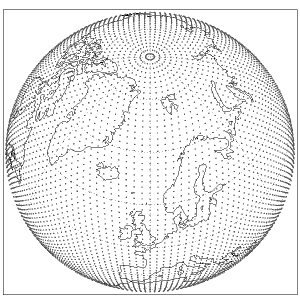
Regular (or full) Gaussian grid
A regular Gaussian grid has the following characteristics:
- there are 4N longitude points along each latitude circle;
- each latitude circle has a grid point at 0o longitude;
- the longitudinal resolution in degrees is 90o/N;
- the points get closer together (i.e. more crowded) as the latitude increases towards the poles;
- the total number of grid points is 8N2.
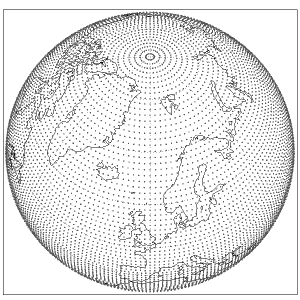
Reduced (or quasi-regular) Gaussian grid
A reduced Gaussian grid:
- has the same number of latitude lines (2N) as the corresponding regular Gaussian grid;
- has a grid point at 0o longitude on each latitude circle;
- has a decreasing number of longitude points towards the poles;
- has a quasi-regular grid spacing in distance at each latitude;
provides a uniform CFL (Courant–Friedrichs–Lewy) condition.
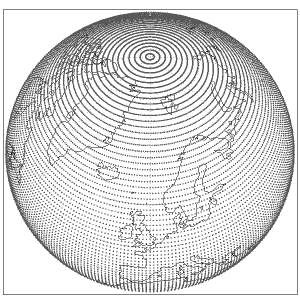
Up to IFS cycle 41r1, ECMWF has used a original reduced Gaussian grid. This has 4N longitude points at the latitude nearest to the equator, with the number of longitude points reducing in blocks as the latitudes approach the poles.
With the planned horizontal resolution increase, ECMWF introduces a slightly different form of the reduced Gaussian grid which is referred to as the octahedral reduced Gaussian grid or, more simply, the octahedral grid.
2 Comments
Riccardo Monfardini
I often see TXXX elsewhere. What grid is this?
Paul Dando
For me at least (some of my colleagues in RD might disagree), TXXX refers to the truncation of the spectral series (which is, of course, related to the grid point resolution). The relationship between the TXXX and OXXX or NXXX grid depends on whether this is a linear grid (usually you see this referred to a TLXXX) or cubic octahedral (referred to as TcoXXX) or (for some very old data) quadratic (TQXXX). See Relationship between spectral truncation and grid point resolution for an explanation.
In short:
I hope this helps.