What is the octahedral grid ?
The octahedral grid has been inspired by the Collignon Projection of the sphere onto an octahedron.
It is a form of reduced Gaussian grid with the same number of latitude lines located at the same latitude values as those of a original Gaussian grid but with the number of longitude points at each latitude circle between the pole and equator computed according to the formula:
\[ \begin{equation*} \mbox{N}_{lat_i} = 4 \times i + 16 \mbox{ for } i = 1, \ldots, \mbox{N} \end{equation*} \]In other words:
- there are 20 longitude points at the latitude circle closest to the poles;
- the number of points increases by 4 at each latitude line from the pole towards the equator.
This is in contrast to the original reduced Gaussian grid where there are 'jumps' between blocks of latitudes with a constant number of longitude points (a restriction imposed by the Fast Fourier Transform routines being used up to IFS cycle 41r1).
As a consequence, the zonal resolution of the octahedral grid varies more with latitude than for the original reduced Gaussian grid. This can be seen in the figures to the right.
Note in particular that the octahedral grid has 4N + 16 longitude points at the latitude circle closest to the equator whereas the original reduced Gaussian grid has 4N longitude points at the latitude circle closest to the equator.
There are also fewer total grid points in the octahedral grid compared to the original reduced Gaussian grid. For example, the O1280 octahedral grid has about 20% fewer grid points than the equivalent N1280 original reduced grid. Generally, an octahedral grid with N latitude lines between the pole and equator has 4xNx(N+9) grid points.
The octahedral grid has been shown to improve the calculation of local derivatives in grid point space.
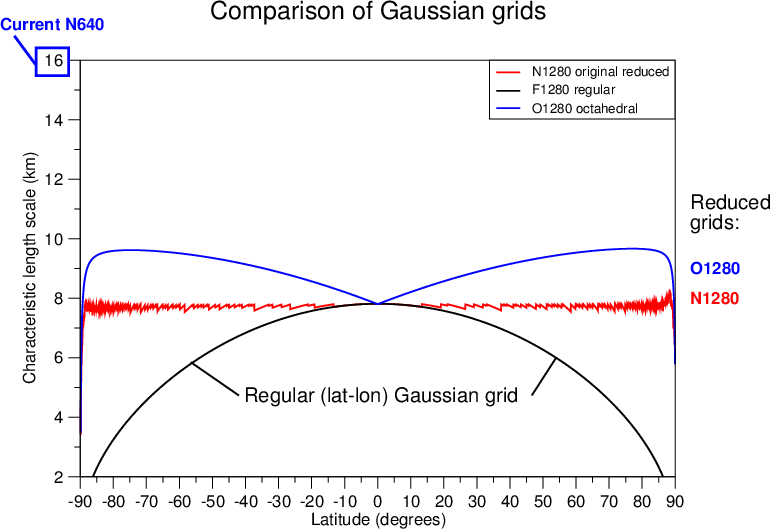
Comparison of the resolution variation with latitude for the reduced Gaussian grids
Variation of the resolution (characteristic length scale) with latitude for the reduced Gaussian grids. The red curve shows the resolution for the original reduced Gaussian grid at N1280 (TC1279). Note that the resolution remains more or less constant at 8km as the latitude varies. The corresponding curve for the O1280 (TCO1279) octahedral grid is shown by the blue curve. The resolution for the O1280 octahedral grid varies from about 8 km at the equator, increasing to about 10 km at 70oN and 70oS before decreasing again towards the poles. The resolution of the N640 original reduced Gaussian grid used for HRES at IFS cycle 41r1 is at about 16 km. Also shown is the regular Gaussian grid at F1280 (black curve).
Comparison of the zonal variation in resolution between original reduced and octahedral grids
Comparison of the zonal variation in resolution for the N1280 original reduced Gaussian grid (left) with the corresponding O1280 octahedral grid (right) on the surface of the sphere
Gaussian grid descriptions
Descriptions of the Gaussian grids introduced for the planned horizontal resolution upgrade and used for HRES and ENS are available:
- HRES: Gaussian grid number 1280
- ENS Days 1 to 15: Gaussian grid number 640
- ENS Extended (Days 16 to 46): Gaussian grid number 320
The descriptions provide the latitude values and the number of longitude points at each latitude for both the original and octahedral reduced Gaussian grids.
The number of points at each latitude is encoded as the PL array in the Grid description section of the GRIB header of a grid point field. This is accessible with grib_api as the pl key.
As of grib_api 1.14.0, a new computed key isOctahedral is introduced which allows users to query the grid type. For an octahedral grid, isOctahedral=1; otherwise, isOctahedral=0.
From grib_api 1.14.4 onwards, the computed key gridName can be used to query the grid name. For an octahedral with 1280 latitudes between pole and equator gridName=O1280; for an original reduced Gaussian grid with 640 latitudes between pole and equator, gridName=N640 while the corresponding regular Gaussian grid has gridName=F640.
Further information
For further background information see:
- Spectral representation of the IFS
- Gaussian grids
- Relationship between spectral truncation and grid point resolution
- Increasing the horizontal resolution
See also:
- Malardel S., et al. 2016: "A new grid for the IFS", ECMWF Newsletter No.146 - Winter 2015/16 (pages 23-28).
- Wedi N.P., 2014: Increasing the horizontal resolution resolution in numerical weather prediction and climate simulations: illusion or panacea ?" Phil. Trans. R.Soc.A, 372, doi: 10.1098/rsta.2013.0289.
Frequently asked questions
Will the change to the octahedral grid affect me if I use regular lat-lon data ?
No, users of regular lat-lon data will be unaffected by the change of model grid. They will, however, benefit from the increase of the model horizontal resolution.
Will ECMWF make data available on the original regular and reduced Gaussian grids ?
Yes, users will still be able to request data, both in dissemination and MARS, on the original regular and reduced Gaussian grids. Note, however, that this will be interpolated from the values on the octahedral reduced Gaussian model grid. See also I make computations involving flux parameters or accumulated fields (for example, to de-accumulate precipitation) and am advised to work on the model grid: which grid should I use ?
I use point data (e.g., for meteograms, vertical profiles, etc) - what do I need to do ?
Users of point data should note that the coordinates of the nearest grid point will have changed. Users should take particular care for coastal points for which the nearest grid point may have changed from a land point to a sea point or vice versa.
Are the new land-sea mask and orography for the octahedral grid available ?
Yes, the new land-sea masks and orography fields for HRES at TCO1279 (O1280), ENS Leg A at TCO639 (O640) and ENS Leg B TCO319 (O320) are available for download:
- HRES: Land-sea mask and orography fields for the O1280 octahedral grid (TCO1279) - UPDATED on 7 December 2015
- ENS Days 1 to 15: Land-sea mask and orography fields for the O640 grid (TCO639) - UPDATED on 7 December 2015
- ENS Extended (Days 16 to 46): Land-sea mask and orography fields for the O320 grid (TCO319) - UPDATED on 7 December 2015
I use the orography in spectral representation - will I be affected ?
Although the spectral resolution for HRES remains constant, the spectral orography has changed. If you have this as a static file then this should be updated with the new version.
Do I need to upgrade the version of GRIB API I use in order to decode data on the octahedral grid ?
Version 1.12.3 of grib_api can decode fields on the octahedral grid correctly. As of grib_api 1.14.0, a new computed key isOctahedral is introduced which allows the grid type to be queried. For the octahedral grid, isOctahedral=1; otherwise, isOctahedral=0.
Can GRIBEX decode data on the octahedral grid ?
GRIBEX is no longer supported by ECMWF and will therefore not be upgraded to support the octahedral grid.
What should I check in my program to make sure it will work with the octahedral grid ?
Any GRIB decoding program that makes use of the PL array to obtain the number of longitude points on each latitude circle should be able to handle the octahedral grid. Programmers should note that the largest number of points at any one latitude circle increases from 4N in the original Gaussian grid to 4N+16 in the octahedral grid and adjust any data structures accordingly to cater for this.
I make computations involving flux parameters or accumulated fields (for example, to de-accumulate precipitation) and am advised to work on the model grid: which grid should I use ?
For performing computations with accumulated fields, users are advised to request data on the octahedral grid.
Is there any change to the vertical resolution as part of the planned resolution upgrade ?
No, only the horizontal resolution is increased. The vertical resolution remains at L137 for HRES and L91 for ENS.
What will happen if I retrieve data from MARS using grid=av ?
Users retrieving data from MARS with the keyword, grid=av ("archived value") will retrieve data on the model grid. For data from the upgraded model this will be the octahedral grid.
What will happen if I retrieve data from MARS using grid=1280 ?
This behaviour is unchanged. By default, users retrieving data from MARS with the keyword, grid=1280 will retrieve data on the regular Gaussian grid with 1280 latitude lines between the pole and equator (equivalent to grid=F1280).
Will ERA-Interim fields also use the cubic octahedral grid ?
No, the horizontal resolution upgrade applies only to ECMWF HRES and ENS operational forecasts, including the monthly extension. It will affect the additional runs in support of the Optional Programme for Boundary Conditions (BC).
Will the ECMWF System 4 Seasonal Forecasts (SEAS) also use the octahedral grid ?
No, the horizontal resolution upgrade applies only to ECMWF HRES and ENS operational forecasts, including the monthly extension.